A fractal is a “series of structures within structures” (10, 11). In addition, they are commonly perceived as a shape that is made from an infinite repeating pattern of that starting shape (1). Since they are self-similar, no matter how much you zoom in, the shape will look likes itself (2). For example, this picture of what is known as a fractal tree is simply created from the repetition of "V" shaped branches. As you can see, there is a single line that acts as the base with two shorter lines going to its left and right side. Off of either of those lines there are slightly shorter lines branching off to its left and right. This is the defining pattern that repeats and creates the fractal.


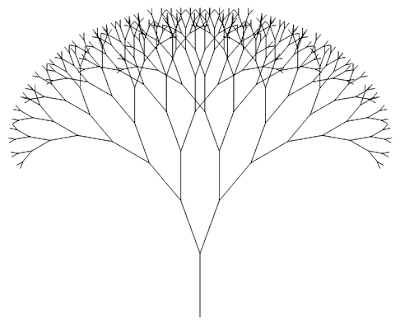
As you might have noticed, objects in nature aren't "'smooth', such as a circle or a triangle, [instead] the shapes that come out of fractal geometry are 'rough' and infinitely complex" (1, 3). This is made possible because fractals have use fractional dimensions. Instead of having a whole numbered dimension, they use decimal dimensions to account for the roughness of the surface of an object (4). When thinking of the dimension of a line, sheet, and cube you know they are 1-D, 2-D, and 3-D. But what does this look like mathematically? What are the numbers you use to actually calculate this? These numbers are found from looking at how the mass of an object changes in proportion to how you scale it. If you cut a line in half, both the scaling factor and mass scaling factor are 1/2. You should also notice that the mass scaling factor is the size scaling factor to the first power, and that a line is only 1-D. (1/2)^1 = 1/2. If you do the same for a 2-D sheet, you will notice that scaling its size down by 1/2 will cause its mass scaling factor to be equivalent to 1/4, which is its scaling size to the second power. (1/2)^2 = 1/4. Likewise, scaling a cube by 1/2 will produce a mass scaling factor of 1/8, or the size scaling factor to the power of its dimension. (1/2)^3 = 1/8. Now it’s time to calculate the dimension of a fractal. Take Sierpinski’s triangle for example, based on the pattern with the shapes above, you know if you scale it down by 1/2 its scaling mass would be 1/2 to the power of it dimension (D). A characteristic of Sierpinski’s triangle is that it is self similar, being made of three smaller copies of itself. You can see this in the image shown below. Therefore, you know that the mass scaling factor is 1/3. Now you have the equation (1/2)^D = (1/3). Performing log base ½ of ⅓ will give you D. This is equivalent to 1.585. The importance of this number is that it gives a way to describe the fractal, considering that the perimeter of a fractal is infinite and the area is 0.
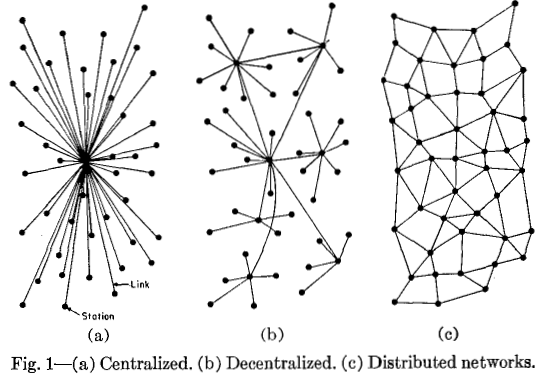
You may not have realized it, but fractals are found everywhere in nature. Look at the picture of this tree for example, it is very similar to the fractal tree shown earlier in that each iteration of additional tree branches are just a skinnier and smaller “V” shaped extension off of the last one. Another example would be of this picture of lighting. If you look closely you can see smaller versions of the main lightning bolt. The reason fractals are so common in nature is because they have the perfect balance between robustness and usefulness. For example, the tree has branches, twigs, leaves, and tissues so that if one segment is infected, destroyed, or otherwise damaged, then the entire tree won’t die. The reason it isn’t a distributed network is because, while a distributed network is more robust, information doesn’t travel nearly as quickly. On the other side is the centralized network, which is very swift, but not very robust. Fractals match the decentralized network structure best because of their design, and basic layout. This is a generalization of why fractals, not necessarily self-similar ones are so common in plants and some animals.



Some of the most famous self-similar fractals include Mandelbröt set, Menger sponge, and Koch snowflake. What is special about artificially made fractals is that they are perfectly self-similar. This means that they infinitely repeat themselves no matter how much you may zoom in on any part of them. This is special because no real patterns in nature perfectly repeat in nature and they eventually end.
The Mandelbröt set is a numbers shown in a 1-D representation. Each input contains two values which make up a complex number. One is a real number and the other an imaginary. Those two values are plugged into the quadratic polynomial (x) = x2 + c (5). Based on the differences between the output of each iteration for that specific complex number, a color will be given. Let’s start at -0.5+0i, where the x is -0.5 and the c is the constant 0i, which equals 0. The first iteration values take the square of -0.5 and add 0 to it, equalling 0.25. To determine the next number in this function, you plug in 0.25 as x, square it, and add 0. This carries on again, plugging in the square of the 0.25 and continues this pattern over and over again. This same pattern is done with every complex number. The point of this function is to determine if it is within the Mandelbröt set. If any of the values of a particular complex number has an absolute value of 0 or go towards 0 then it is part of the set.
Another well known fractal is the Menger sponge. It is a simple pattern created by separating a cube into twenty seven equivalent cubes and omitting the center ones on each face and the very center one within the cube (6). Do the same thing to these eight remaining cubes. Continue splitting the cubes into twenty seven parts and omitting the center ones to create your fractal!




